Dugó van? Bontsátok el a városi autópályákat!

Szöul, 2005. Csupán két évvel a projekt indulását követően elkészül és átadják a város egyik legnagyobb megújulási programját: a Cheonggyecheon folyó megnyitását. Sok városlakó ekkorra valószínűleg már rég elfeledte, vagy talán sosem tudta, hogy a folyó, amely jó harminc évig már csak autóból volt látható, egykor a város kellős közepén át folyt. Ahogy a képeken is látszik, igen figyelemre méltó a nyereség a városépítészeti minőségben. A néhány megmaradt autópálya-maradvány alig néhány évvel később már régmúlt idők romjainak tűnik.

Hogyan tovább? Jópofának tűnik. De egy teljes autópályát lebontani? Nem fog belefulladni Szöul többi része az autók tengerébe? Nos, legalábbis nem jobban, mint előtte. Valóban, néhány kritikus csodálkozva dörzsölte a szemét, amikor kiderült, hogy az autópálya eltávolítását követően a városban a forgalom áramlása generálisan javult, sőt, az átlagos menetidők csökkentek.

Mivel magyarázható ez? A szöuli autópálya elbontásának váratlan sikere a Braess-paradoxon jó példája. Ugyanis a Braess-paradoxon áll az először megdöbbentőnek tűnő hatás mögött. Szívesen emlegeti ezt a példát Michael Siebert matematikus, az automatizált menetrendi optimalizálás szakértője is. A http://kerekparosmiskolc.net/wp-content/plugins/wp-external-links/images/ext-icons/ext-icon-13.png); text-decoration: none; color: rgb(255, 0, 0); background-position: 100% 50%; background-repeat: no-repeat no-repeat;”>Future Mobility Camp alkalmával a paradoxont az itt következő, egyszerű modellszámítással személtette.

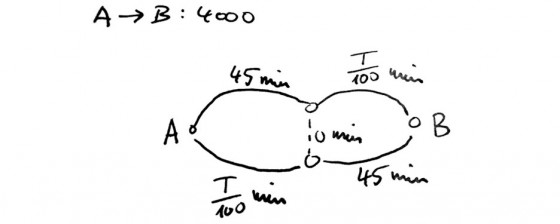
A és B pontokat két útvonal köti össze. A két szakasz rendszeres forgalma 4000 jármű. Az út egyik részén, felül a második, alul az első részen, a menetidő mindig a járművek számától függ. Összesen 45 perc plusz a járművek száma(T)/100 perc. Bizonyos idő után egyensúly áll be – hiszen amikor egy jármű útvonalat váltana, mindig a mindenkori másik útvonal válna gyorsabbá, úgyhogy egy másik jármű megintcsak ezt választaná. Az eljutási idő az egyensúlyi állapotban mindenki számára 65 perc (45+2000/100).

Fölmerül az ötlet, hogy összeköttetést létesítsenek a két útvonal között. Ez időnyereséget hozna? Dehogy! Miután megépül az összeköttetés, amelynél sokat nyomott a latba a modellben a 0 perces hipotetikus utazási idő, a járművek hirtelen 80 perc alatt, azaz 15 perccel hosszabb idő alatt érik el A-ból B-t. Szép eredmény? Nézzük, hogyan járják útjukat a közlekedők: az első szakasz megtételéhez mindig gyorsabb az alsó szakasz: 4000/100 = 40 perc kevesebb, mint a 45 perc, amely a felső szakaszon szükséges. Középre érkezve, ugyanez lesz a döntés, most a felső szakasz javára. A maximum 40 perc itt is kiüti a 45 percet. B-be érkezve azonban, mind a 4000 jármű 15-15 perccel tovább volt úton, mint az összeköttetés megépülte előtt, ez összesen 1000 óra többlet.

Lehetséges mindez egy jól átgondolt modellben? Nem. “A Braess-paradoxon véletlenszerű hálózatokban 50%-os valószínűséggel lép föl.” – magyarázza Michael. Másképpen fogalmazva: ha egy véletlen-generátorral helyekből és utakból álló hálózatot hozunk létre (ezek a gráfelméletben csúcsokként és élekként ismertek), akkor minden második hálózatban lesz legalább egy út, amely a hálózatban negatívan hat az eljutási időre. Hoppá! Könnyen lehetséges, hogy városaink tele vannak utcákkal, amelyek objektíven vizsgálva önmagában a létezésükkel lassítják a forgalmat.

Már egy másik kitűnő példa is kirajzolódni látszik. New York Cityben a legutóbbi években a Broadway (mely átlós összeköttetés New York utcáinak egyébként derékszögű hálózatában) egyes részeit szakaszosan lezárták a gépjárművek forgalma elől, ezek a gyalogosok és kerékpárosok számára felértékelődtek. Az első megfigyelések alapján itt is kedvező hatások mutatkoznak a gépjárműforgalomban is.

A német blog végezetül felteszi a kérdést: mi van Berlinben? Vajon a délkeleti útépítési projektre nem lesz-e igaz a Braess-paradoxon?
Mi pedig, itt, Miskolcon azt várjuk, hogy hozzánk is elérjen a korszerű tervezői, városfejlesztői gondolkodás, hogy itt is a fenntarthatóság, a város élhetősége váljék végre a városfejlesztés vezérfonalává.

Német nyelvű szöveg és a képek forrása: http://kerekparosmiskolc.net/wp-content/plugins/wp-external-links/images/ext-icons/ext-icon-13.png); text-decoration: none; color: rgb(255, 0, 0); background-position: 100% 50%; background-repeat: no-repeat no-repeat;”>Alle Macht den Rädern blog